Synthetic ambient noise and noise cross-correlations
Contents
1. Background
Ambient noise tomography has been a very popular imaging strategy of investigating the earth’s interior in past over two decades. The basic principle of this method is that stacked cross-correlations from noise recordings made by two receivers can be approximately the Green’s function from one receiver to another. We have the need of synthesizing ambient noise for validating this important idea, or exploring characteristics of ambient noise. Here we introduce a simple way of computing synthetic ambient noise.
2. Steps to doing synthetics
2.1 Configuring the receiver and source positions
Firstly we randomly generate source and receiver positions with given coordinate ranges using the following python codes:
|
|
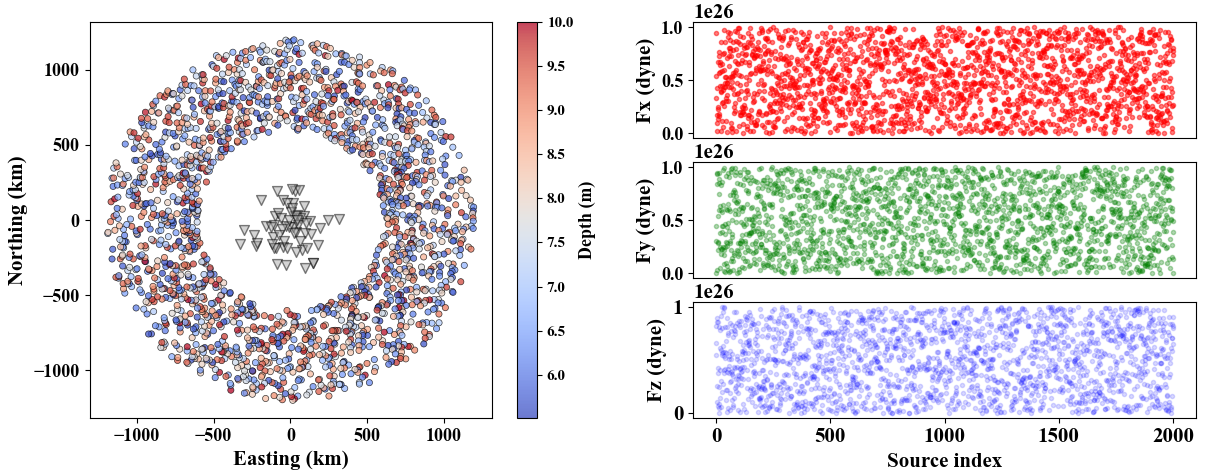
We generated 60 receivers within the circle with radius of ~250 km, and coordinates are saved in rec.txt.
Now we generate 2001 sources within a ring belt with radius limitations of 600 km and 1200km, and three-component forces.
Note that source positions are stored in file src.txt, and force components are saved in file force.txt.
|
|
The receiver and source configuration is shown by the following figure.
|
|
2.2 Synthetic ambient noise
The ambient noise recordings can be considered as the wavefield excited by many events, like the primary and secondary microseisms from interactions between ocean waves and our solid earth, and maybe some weak seismic signals generated by small earthquakes. These events randomly occur in time and space. Therefore, we compute seismic waveforms triggered by many earthquakes, and randomly stack these earthquake-generated waveforms according to event occuring time and their positions. Finally we synthesize ambient seismic noise. The python codes of computing waveforms excited by earthquakes:
|
|
Now we synthesize ambient noise with the following codes:
|
|
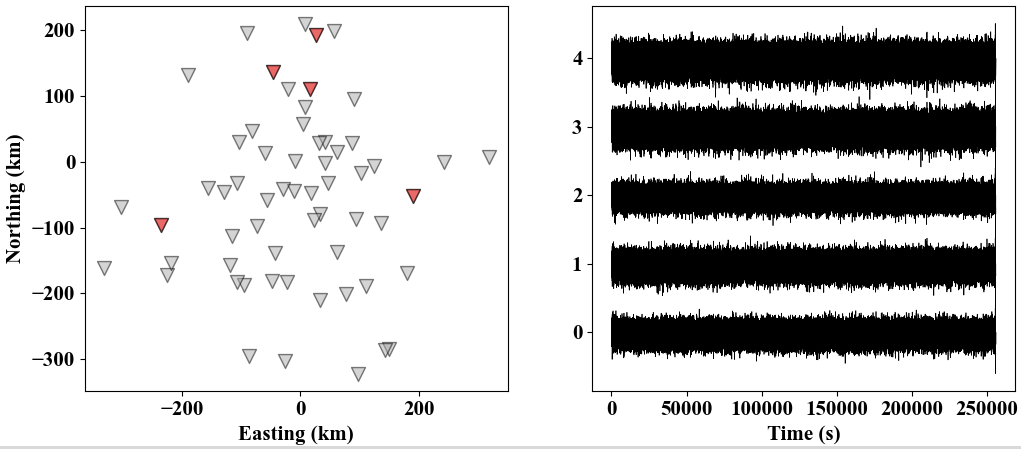
We randomly choose synthetic ambient noise waveforms from 5 receivers to visualize:
|
|
3. Checking the relation between receiver-pair cross-correlation and the green’s function
Ideal source distribution (energy equipartion in all directions) can lead to the phase smilarity between stacked cross-correlations and the Green’s functions. For detail, the relation is given by $$ G_{AB}(t) = -\frac{dC_{AB}(t)}{dt}=\frac{dC_{AB}(-t)}{dt}, \tag{1} $$ where, $G_{AB}(t)$ and $C_{AB}(t)$ are separately the Green’s function and stacked cross-correlation between receiver A and B. Now we compute the temporally average cross-correlation function between receivers.
|
|
Here we compare the empirical green’s function from cross-corrlation and corresponding Green’s function with distance of ~ 500 km on different frequency bands.
|
|
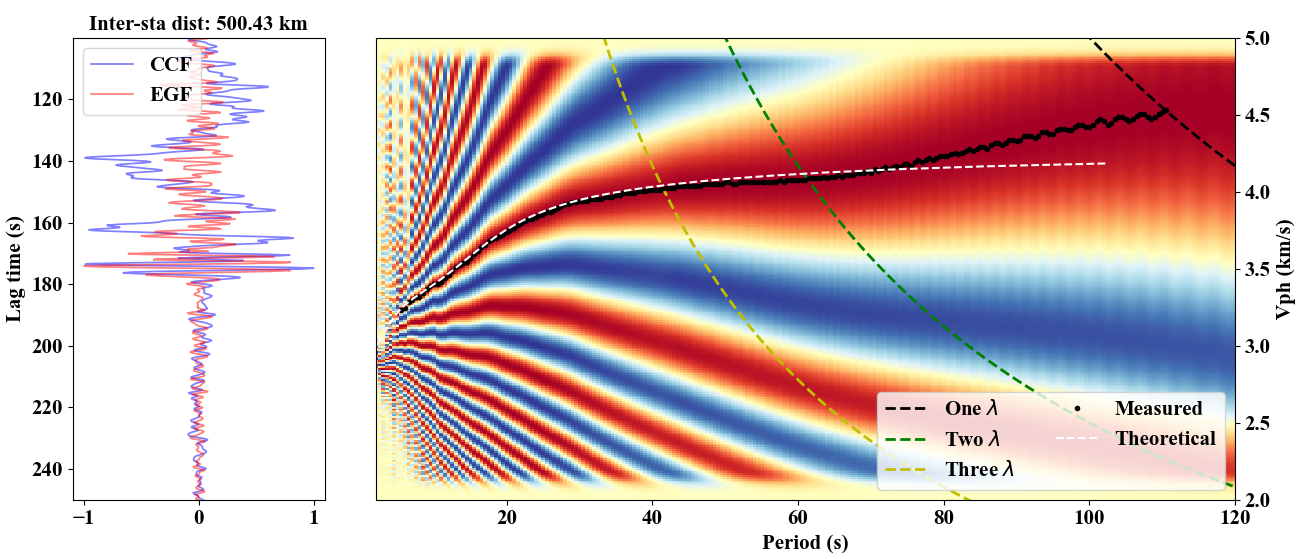
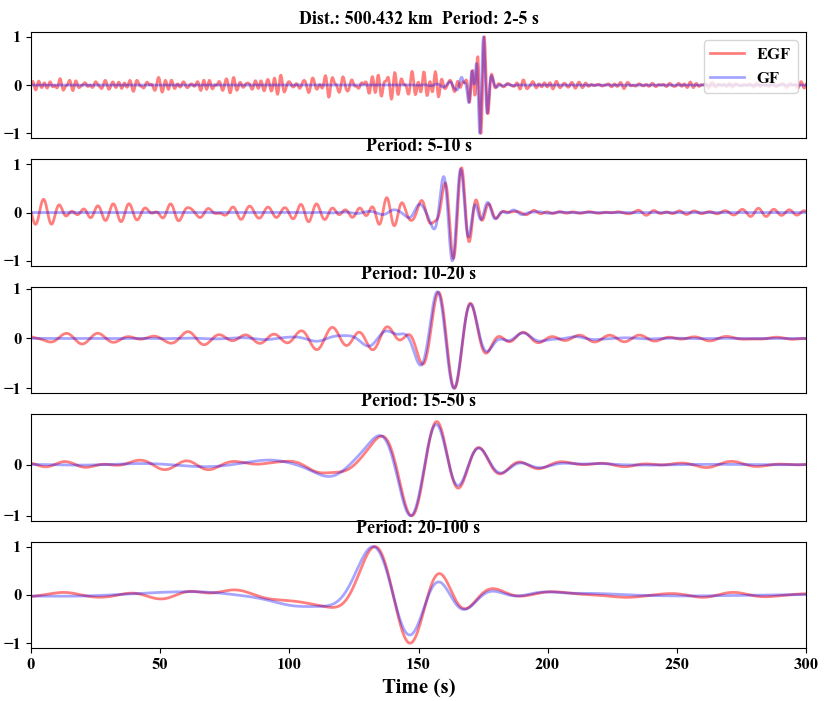 The cross-correlation and Green’s function waveforms are very similar on different period ranges. Furthermore,
we use the image transform technique (Yao et al., 2006) to estimate dispersion curve from the cross-correlation function,
and compare it with the theoretical one.
The cross-correlation and Green’s function waveforms are very similar on different period ranges. Furthermore,
we use the image transform technique (Yao et al., 2006) to estimate dispersion curve from the cross-correlation function,
and compare it with the theoretical one.
|
|
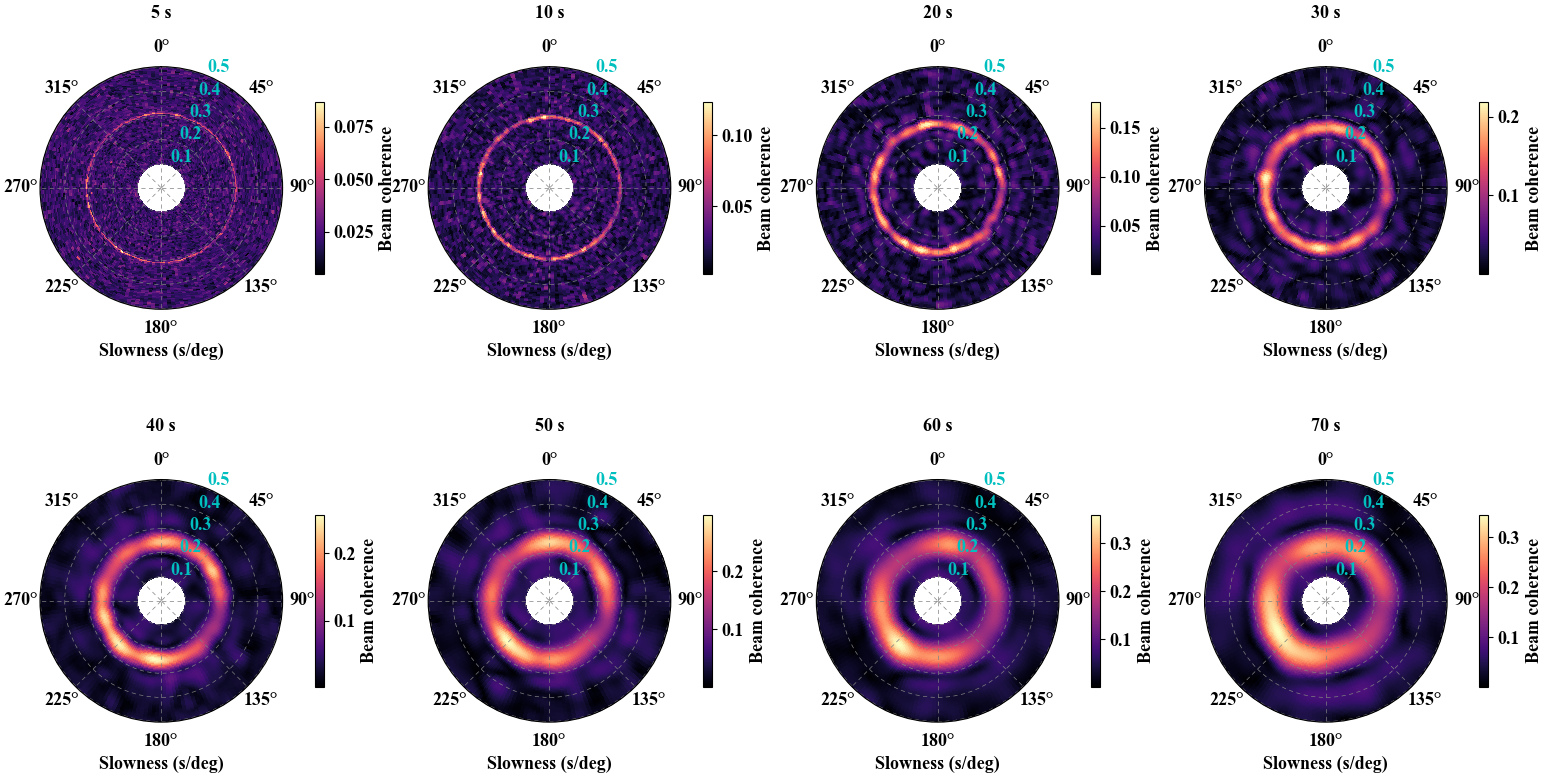
4. Noise source distribution from beamforming analysis
We utilize the beamforming array method to detect back-azimuth and slowness of noise sources to explore whether these sources come from all directions.
|
|
References
Yao, H., R. D. van der Hilst, and M. V. de Hoop (2006), Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis—I. Phase velocity maps, Geophys. J. Int., 166, 732 – 744, doi:710.1111/j.1365-1246X.2006.03028.x
Author geophydog
LastMod 2024-01-29
