1 One-way filtering

For given filter transfer function $H(\omega)$, the filtered data $X_1(\omega)$ is $$ \begin{cases} X_1(\omega) &= H(\omega) \cdot X(\omega)\\
x_1(t) &= \mathscr{R} \{ \mathscr{F}^{-1}[X_1(\omega)] \} \end{cases} \tag{1}. $$ Eq. $(1)$ is called $one-way$ filtering, and it ensure that the onsets of original and filtered signals are at the same moment.

2 Two-way filtering

However, if we want to ensure that the peaks of original and filtered signals are at the same moment, we need to filter again, which is named $two-way$ filtering. $$ \begin{cases} X_2(\omega) &= \mathscr{F} \{ Reverse [x_1(n)] \} \cdot H(\omega)\\
x_2(t) &= Reverse \{ \mathscr{R} \{ \mathscr{F}^{-1}[X_2(\omega)] \} \} \end{cases} \tag{2}. $$

Here, we give an example to show these two types of filters.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import iirfilter, zpk2sos, sosfilt
from scipy import fft

def lowpass(d, fs, fc, orders=4, zerophase=False, taper=0.01):
    n = len(d)
    fd = fft.fft(d)
    f = np.arange(n) * fs / n
    w = 2 * np.pi * f / fs
    wc = 2 * np.pi * fc / fs
    k = np.arange(2*orders)
    if orders % 2 == 0:
        q = np.tan(wc/2) * np.exp(1j*(k+0.5)/orders*np.pi)
    else:
        q = np.tan(wc/2) * np.exp(1j*k/orders*np.pi)
    p = (1 + q) / (1 - q)
    z = np.exp(1j*w)
    h = np.ones_like(w, dtype=complex)
    for pp in p[abs(p)<1]:
        h *= ((1-pp)  / (1-pp/z))
    h *= ( (1+1/z) ** orders / 2**orders )
    dd = fft.ifft(fd * h).real
    if zerophase:
        dd = fft.ifft(fft.fft(dd[::-1])*h)[::-1].real
    ni = int(n*taper)
    k1 = np.arange(ni)
    k2 = (-k1)[::-1]
    ta1 = np.cos(np.pi*k1/ni/2) ** N
    ta2 = np.cos(np.pi*k2/ni/2) ** N
    dd[:ni] *= ta2
    dd[-ni:] *= ta1
    return f, h, dd

n = 500
dt = 0.05
t = np.arange(n) * dt
fs = 1 / dt
fc = 1
N = 4
d1 = np.zeros(n)
d1[n//2-10: n//2+1] = 1/10*np.arange(n//2-10, n//2+1) + (20-n)/20
d1[n//2: n//2+11] = -1/10*np.arange(n//2, n//2+11) + (20+n)/20
f, h, d3 = lowpass(d1, fs, fc, orders=N, zerophase=True, taper=0.01)
_, _, d2 = lowpass(d1, fs, fc, orders=N, zerophase=False, taper=0.01)
z, p, k = iirfilter(N, 2*fc/fs, btype='lowpass', ftype='butter', output='zpk')
sos = zpk2sos(z, p, k)
d4 = sosfilt(sos, d1)
d5 = sosfilt(sos, d4[::-1])[::-1]

plt.figure(figsize=(10, 5))
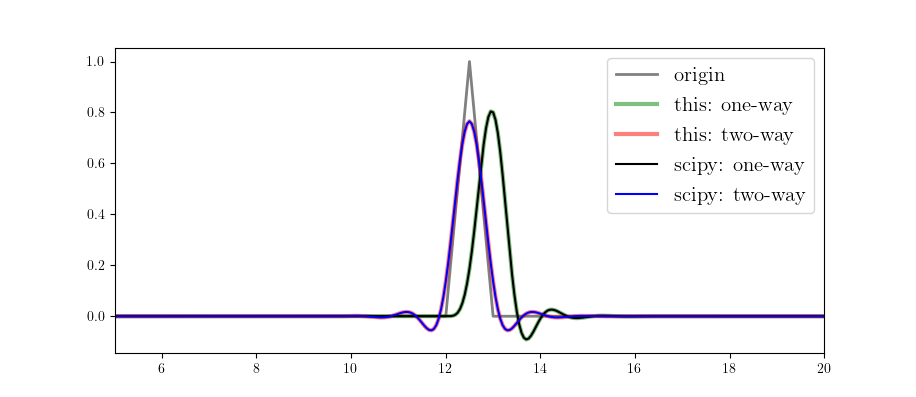
plt.plot(t, d1, 'gray', lw=2, label='origin')
plt.plot(t, d2, 'g', lw=3, label='this: one-way', alpha=0.5)
plt.plot(t, d3, 'r', lw=3, label='this: two-way', alpha=0.5)
plt.plot(t, d4, 'k', lw=1.5, label='scipy: one-way')
plt.plot(t, d5, 'b', lw=1.5, label='scipy: two-way')
plt.legend(fontsize=15)
plt.show()

One-two-way-filter