Butterworth filters

$$ |H(w)|^2=\frac{1}{1+( \frac{tan\frac{\omega}{2}} {tan\frac{\omega_c}{2}})^{2N}} \tag{1} $$

Low-pass filter

Given the attenuation values $A_c$ and $A_r$ at cut-off frequencies $\omega_c$ and $\omega_r$, respectively, we first calculate the orders $N$ of filter. We know, $$ \begin{aligned} A_r &= -20lg|H(\omega_s)|\\
&= -20lg\frac{1}{\sqrt{1+(\frac{tan\frac{\omega _r}{2}}{\frac{\omega_c}{2}})^{2N}}} \end{aligned} \tag{2}, $$ and the orders $N$ is given by $$ N = \frac{1}{2}\frac{lg(10^{\frac{A_r}{10}}-1)}{lg(\frac{tan\frac{\omega_r}{2}}{tan\frac{\omega_c}{2}})} \tag{3}. $$ However, if you give the filter orders $N$, it can control the width of transition band of the filter.

We rewrite eq. $(1)$ as $$ |H(\omega)|^2 = \frac{tan^{2N}\frac{\omega_c}{2}}{tan^{2N}\frac{\omega_c}{2}+tan^{2N}{\frac{\omega}{2}}} \tag{4} $$ and according to the $Euler’s$ formula $e^{j\theta}=cos\theta+jsin\theta$, we have $$ \begin{aligned} tan\frac{\omega}{2} &= \frac{sin\frac{\omega}{2}}{cos\frac{\omega}{2}}\\
&= \frac{1}{j}\frac{ e^{j\frac{\omega}{2}}-e^{-j\frac{\omega}{2}} } { e^{j\frac{\omega}{2}}+e^{-j\frac{\omega}{2}} }\\
&= \frac{1}{j}\frac{ 1-e^{-j\omega} } { 1+e^{-j\omega} } \end{aligned} \tag{5}. $$ Let $z=e^{-j\omega}$, and combine eq. $(5)$ to yield $$ |H(z)|^2 = \frac{tan^{2N}\frac{\omega_c}{2}} {tan^{2N}\frac{\omega_c}{2}+(-1)^N(\frac{1-z^{-1}}{1+z^{-1}})^N} \tag{6}. $$ We know there are $N$ repeated zeros, namely, $-1$, of this transfer function and we calculate the poles as follows. $$ q_k= \frac{1-z_k^{-1}}{1+z_k^{-1}}= \begin{cases} &tan\frac{\omega_c}{2}e^{j\frac{2k+1}{2N}\pi}, \text{ for } N \text{ is even, and }k=0, 1, 2, \cdots, 2N-1;\\
&tan\frac{\omega_c}{2}e^{j\frac{k}{N}\pi}, \text{ for } N \text{ is odd and }k=0, 1, 2, \cdots, 2N-1. \end{cases} \tag{7}. $$ We get $$ z_k = \frac{1+q_k}{1-q_k} \tag{8}. $$ Lastly, the transfer function can be calculated by $$ H(z) = \frac{1}{2^N}\frac{\prod_{|z_k|<1}(1-z_k)(1+z^{-1})^N}{\prod_{|z_k|<1}(1-z_kz^{-1})} \tag{9}. $$ Here, we separately give attenuation values $3 \ dB$ and $30 \ dB$ at cut-off frequency $\omega_c$ and stop frequency $\omega_r$ to show the frequency response. 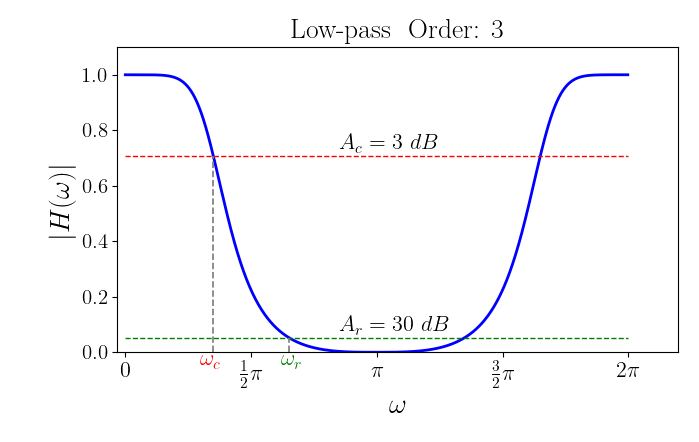low-pass

We give a python code example of implementing a low-pass filter and compare this result with that filtered by the butterworth filter in scipy.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

import numpy as np
import matplotlib.pyplot as plt
from obspy import read
from scipy.signal import butter, filtfilt
from scipy import fft

def lowpass(d, fs, fc, orders=4, zerophase=False, taper=0.01):
    n = len(d)
    fd = fft.fft(d)
    f = np.arange(n) * fs / n
    w = 2 * np.pi * f / fs
    wc = 2 * np.pi * fc / fs
    k = np.arange(2*orders)
    if orders % 2 == 0:
        q = np.tan(wc/2) * np.exp(1j*(k+0.5)/orders*np.pi)
    else:
        q = np.tan(wc/2) * np.exp(1j*k/orders*np.pi)
    p = (1 + q) / (1 - q)
    z = np.exp(1j*w)
    h = np.ones_like(w, dtype=complex)
    for pp in p[abs(p)<1]:
        h *= ((1-pp)  / (1-pp/z))
    h *= ( (1+1/z) ** orders / 2**orders )
    dd = fft.ifft(fd * h).real
    if zerophase:
        dd = fft.ifft(fft.fft(dd[::-1])*h)[::-1].real
    ni = int(n*taper)
    k1 = np.arange(ni)
    k2 = (-k1)[::-1]
    ta1 = np.cos(np.pi*k1/ni/2) ** N
    ta2 = np.cos(np.pi*k2/ni/2) ** N
    dd[:ni] *= ta2
    dd[-ni:] *= ta1
    return f, h, dd


tr = read()[0]
dt = tr.stats.delta
fs = 1 / dt
d1 = tr.data.copy()
n = len(d1)
t = np.arange(n) * dt
fc = 2.5
fr = 1.5
Ar = 30
N = 4
f, h, d2 = lowpass(d1, fs, fc, orders=N, zerophase=True, taper=0.01)
[b, a] = butter(N, 2*fc/fs, 'lowpass')
d3 = filtfilt(b, a, d1)

plt.figure(figsize=(10, 5))
plt.plot(t, d2, 'r', lw=3, label='this')
plt.plot(t, d3, 'b', lw=1.5, label='scipy')
plt.legend(fontsize=15)
plt.show()

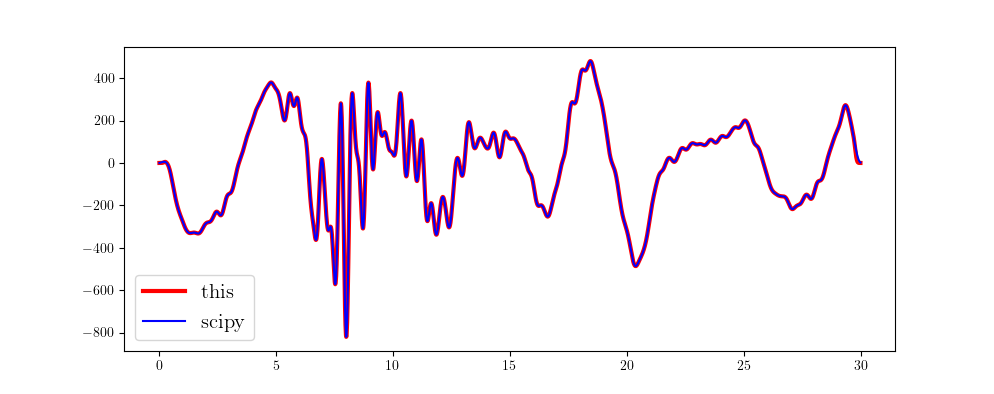Low-pass-wave This result perfectly agrees with that in scipy, doesn’t it?