1 Basic princeples

For a Butterworth high-pass filter, the squared frequency response is given by $$ |H(\omega)|^2 = \frac{1}{1+(\frac{tan\frac{\omega_c}{2}}{\frac{\omega}{2}})^{2N}} \tag{1}. $$ Using $tan\frac{\omega}{2}=\frac{1}{j}\frac{1-e^{-j\omega}}{1+e^{-j\omega}}$ and $z=e^{-j\omega}$, we have $$ |H(z)|^2=\frac{(-1)^N(\frac{1-z^{-1}}{1+z^{-1}})^{2N}}{(-1)^N(\frac{1-z^{-1}}{1+z^{-1}})^{2N}+tan^{2N}\frac{\omega_c}{2}} \tag{2}. $$ We know there $N$ repeated zeros $1$ of this transfer function, and the poles are little bit complicated. We first calculate $q_k=\frac{1-z_k^{-1}}{1+z^{-1}}$. $$ q_k= \begin{cases} &tan\frac{\omega_c}{2}e^{j\frac{2k+1}{2N}\pi}, \text{ for } N \text{ is even and }k=0, 1, 2, \cdots, 2N-1;\\
&tan\frac{\omega_c}{2}e^{j\frac{k}{N}\pi}, \text{ for } N \text{ is odd and }k=0, 1, 2, \cdots, 2N-1. \end{cases} \tag{3}, $$ and $z_k=\frac{1+q_k}{1-q_k}$. The transfer function of a Butterworth high-pass filter is given by $$ H(z)= \frac{1}{2^N}\frac{\prod_{|z_k|<1}(1+z_k)(1-z^{-1})^N}{\prod_{|z_k|<1}(1-z_kz^{-1})} \tag{4}. $$

2 Python code

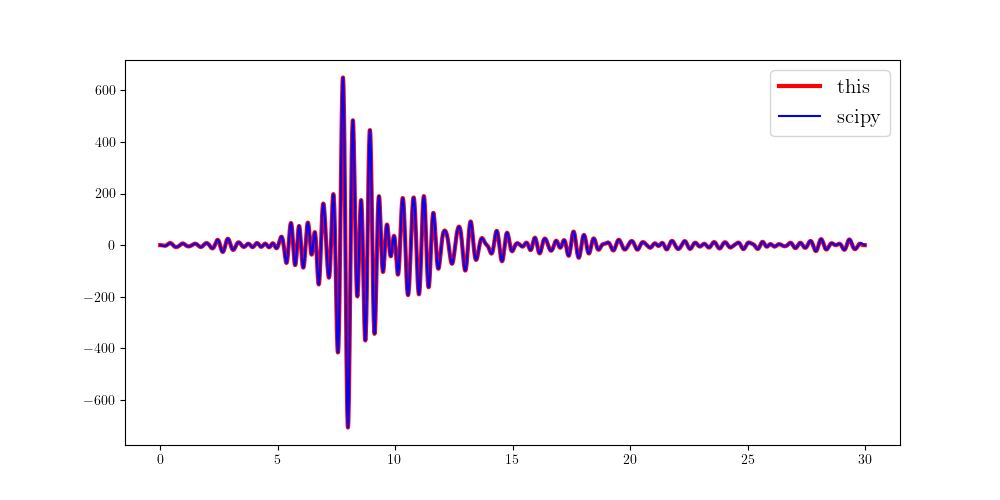
Here, we give an example of implementing the Butterworth high-pass filter and compare it with that generated by scipy.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import numpy as np
import matplotlib.pyplot as plt
from obspy import read
from scipy.signal import butter, filtfilt
from scipy import fft

def highpass(d, fs, fc, orders=4, zerophase=False, taper=0.01):
    n = len(d)
    f = np.arange(n) * fs / n
    w = 2 * np.pi * f / fs
    wc = 2 * np.pi * fc / fs
    k = np.arange(2*orders)
    if orders % 2 == 0:
        q = np.tan(wc/2) * np.exp(1j*(k+0.5)/orders*np.pi)
    else:
        q = np.tan(wc/2) * np.exp(1j*k/orders*np.pi)
    p = (1 + q) / (1 - q)
    z = np.exp(1j*w)
    h = np.ones_like(w, dtype=complex)
    for pp in p[abs(p)<1]:
        h *= ((1+pp)  / (1-pp/z))
    h *= ((1-1/z) ** orders / 2**orders)
    dd = fft.ifft(fft.fft(d) * h).real
    if zerophase:
        dd = fft.ifft(fft.fft(dd[::-1])*h)[::-1].real
    ni = int(n*taper)
    k1 = np.arange(ni)
    k2 = (-k1)[::-1]
    ta1 = np.cos(np.pi*k1/ni/2) ** N
    ta2 = np.cos(np.pi*k2/ni/2)  ** N
    dd[:ni] *= ta2
    dd[-ni:] *= ta1
    return f, h, dd

tr = read()[0]
tr.filter('bandpass', freqmin=0.5, freqmax=3, corners=4, zerophase=True)
dt = tr.stats.delta
fs = 1 / dt
d1 = tr.data.copy()
n = len(d1)
t = np.arange(n) * dt
fc = 1.5
N = 4
f, h, d2 = highpass(d1, fs, fc, orders=N, zerophase=True, taper=0.01)
[b, a] = butter(N, 2*fc/fs, 'highpass')
d3 = filtfilt(b, a, d1)

plt.figure(figsize=(10, 5))
plt.plot(t, d2, 'r', lw=3, label='this')
plt.plot(t, d3, 'b', lw=1.5, label='scipy')
plt.legend(fontsize=15)
plt.show()

High-pass filter