1 Introduction

The $Fourier \ Transform$ convert the signal in one domain to another domain, for instance from time domain to frequency domain. The definition of $Fourier \ Transform$ is given by $$ X(\omega) = \int_{-\infty}^\infty x(t)e^{-i \omega t} \tag{1}. $$

For the operation in programming, we need its discrete form, namely, $$ X(k) = \sum_{n=0}^{N-1}x(n) e^{\frac{-i2\pi kn}{N}} \tag{2}, $$ where, $k$ is the index of the $k_{th}$ frequency point, and we can find the $k_{th}$ frequency like this $$ f_k = \frac{kf_s}{N} \tag{3}, $$ $f_s$ is sampling rate of signal and $f_s=\frac{1}{\Delta t}$.

1
2
3
4
5
6
7

import numpy as np
n = 1024
x = np.random.randn(n)
fft np.zeros_like(x, dtype=complex)
xn = np.range(n) / n
for k in range(n):
	fft[k] = sum( np.exp(-1j*2np.pi*k*xn) )

Actually, we have $$ X(k) = X^*(N-k) \tag{4}, $$ where, $^*$ means the complex conjugate. Here, we show how how eq. $(4)$ comes. $$ \begin{aligned} X(N-k) &= \sum_{n=0}^{N-1}x(n)e^{-\frac{-i2\pi (N-k)n}{N}}\\
&= \sum_{n=0}^{N-1}x(n)e^{\frac{-i2\pi N}{N}}e^{\frac{i2\pi kn}{N}}\\
&= \sum_{n=0}^{N-1}x(n)e^{\frac{i2\pi kn}{N}}\\
&= X^*(k) \end{aligned} \tag{5}. $$ Eq. $(4)$ suggests that we only need to compute the first half of $X(k), k=0, 1, 2, \cdots, \frac{N}{2}$.

2 FFT in Python

However, we just call the methods of libraries Numpy and Scipy in Python to implement $Fourier \ Transform$ as follows,

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

import numpy as np
from scipy import fft

n = 1024
x = np.random.randn(n)
# using fft of numpy.
fft1 = np.ft.fft(x)

# using fft of scipy.
fft2 = fft.fft(x)

3 Code demo

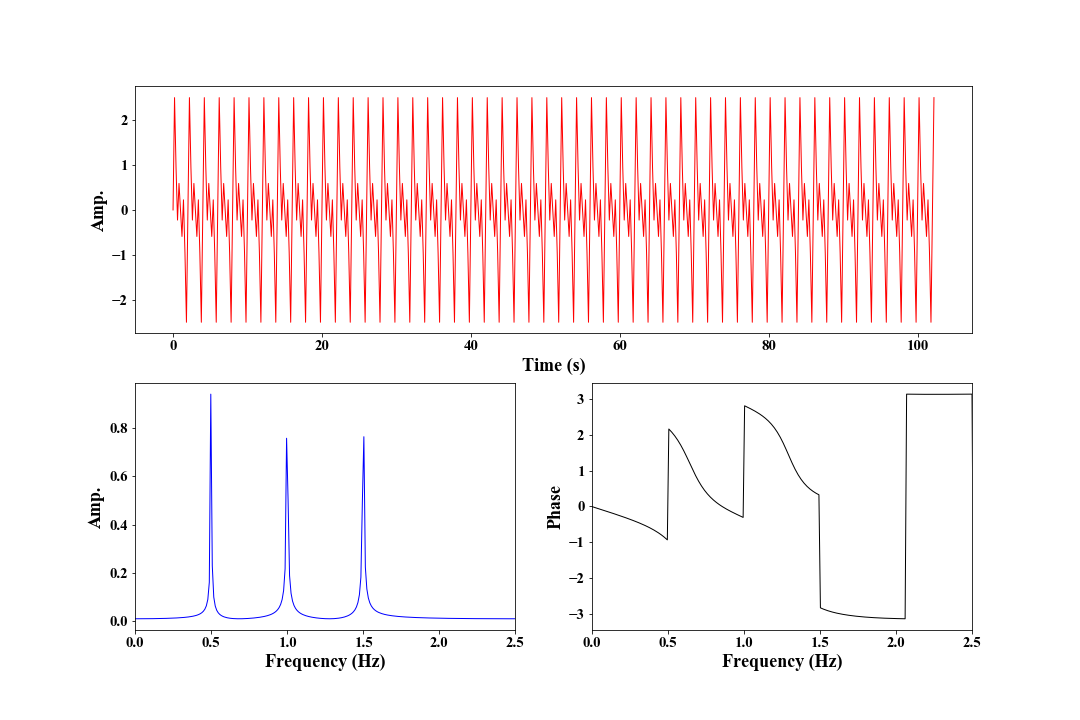
Here, we give an example to show how to convert a real signal in time domain to frequency domain.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

import numpy as np
import matplotlib.pyplot as plt

n = 512
dt = 0.2
fs = 1 / dt
t = np.arange(n) * dt
f = np.arange(n) * fs / n
m = 3
# We generate a signal with frequencies (0.5, 1.0, 1.5).
s = np.zeros(n)
for i in range(m):
    s += np.sin(2*np.pi*(i+1)*0.5*t)

# Get the FFT of s
fd = np.fft.fft(s) / n * 2
# The amplitude spectrum.
fa = abs(fd)
# The phase spectrum.
fp = np.arctan2(fd.imag, fd.real)

plt.figure(figsize=(15, 10))
plt.subplot(211)
plt.plot(t, s, 'r', lw=1)
plt.xlabel('Time (s)', fontsize=18)
plt.ylabel('Amp.', fontsize=18)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)

plt.subplot(2, 2, 3)
plt.plot(f, fa, 'b', lw=1)
plt.xlim(0, fs/2)
plt.xlabel('Frequency (Hz)', fontsize=18)
plt.ylabel('Amp.', fontsize=18)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.subplot(2, 2, 4)
plt.plot(f, fp, 'k', lw=1)
plt.xlim(0, fs/2)
plt.xlabel('Frequency (Hz)', fontsize=18)
plt.ylabel('Phase', fontsize=18)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.show()

The following figure shows the FFT of $x$. FFT-01.png